Hamming distance

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (May 2015) (Learn how and when to remove this message)

Hamming distance

4-bit binary tesseract for finding Hamming distance. Two example distances: 0100→1001 has distance 3; 0110→1110 has distance 1
Class	String similarity
Data structure	string
Worst-case performance	${\displaystyle O(n)}$
Best-case performance	${\displaystyle O(1)}$
Average performance	${\displaystyle O(n)}$
Worst-case space complexity	${\displaystyle O(n)}$

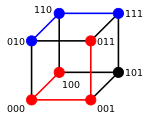
3-bit binary cube for finding Hamming distance

Two example distances: 100→011 has distance 3; 010→111 has distance 2

The minimum distance between any two vertices is the Hamming distance between the two binary strings.

In information theory, the Hamming distance between two strings or vectors of equal length is the number of positions at which the corresponding symbols are different. In other words, it measures the minimum number of substitutions required to change one string into the other, or equivalently, the minimum number of errors that could have transformed one string into the other. In a more general context, the Hamming distance is one of several string metrics for measuring the edit distance between two sequences. It is named after the American mathematician Richard Hamming.

A major application is in coding theory, more specifically to block codes, in which the equal-length strings are vectors over a finite field.